毛捷等:复杂网络在地方公共债务风险研究中的应用
内容提要:本文首先介绍财政金融风险的传统研究方法。通过梳理归纳发现,传统风险分析方法有其特定的适用范围和前提条件,具有一定局限性。基于此,本文系统阐述了新兴的风险分析方法——复杂网络在地方公共债务风险研究中的进展。研究发现,网络拓扑结构、网络生成模型以及网络类型等会对地方公共债务风险网络的传染路径和演变过程产生重要影响。本文的研究为深入开展地方公共债务风险研究、科学制定债务风险防范措施提供了方法参考。
一、引言
2008年全球金融危机爆发后,为配合经济刺激计划的实施,中国各部门债务规模持续增长,尤其是以政府性债务为主的地方公共债务呈爆发式增长,风险隐患凸显,引起社会各界高度关注。《国务院关于进一步深化预算管理制度改革的意见》(国发〔2021〕5号)提出,防范化解地方政府债务风险是重要的政治纪律和政治规矩。在此背景下,如何进一步优化地方公共债务风险防控的效果已成为当前亟待解决的重要课题。
地方公共债务风险是财政风险和金融风险的联结点(毛捷等,2019;周世愚,2021)。从纳入预算管理的法定债务看,由于地方政府债券的持有者主要是商业银行等金融机构,地方政府债券引发的风险将直接向金融系统转移。从未纳入预算管理的隐性债务看,地方政府隐性债务具有融资工具多样化、风险来源多元化以及交易结构复杂化等特征,其引发的风险往往会在财政部门与金融部门之间交互传染。因此,地方公共债务的风险研究不能局限于财政系统内部,也应同时分析债务风险溢出导致的金融风险。
财政金融风险的传统研究方法,比如在险价值法、广义条件异方差模型以及风险指标法等,在风险测算和预警等方面作出了重要贡献,但存在假设条件严格、模型设定与现实中日益复杂的市场情况脱节等不足,而且这类方法主要关注个体之间的局部联系,难以系统地、动态地分析风险的传染过程和演变规律。因此,对于财政金融风险交织的地方公共债务,传统的风险分析方法往往难以准确分析这类债务的风险传染效应和扩散过程。
复杂网络作为一种新兴的风险分析方法,凭借其假设条件少、模型设定与金融市场现实情况更为贴近等优势,能较好地识别地方公共债务引发的财政风险与金融风险叠加共振的效应。随着地方公共债务规模持续扩大,尤其是地方政府隐性债务的增长,政府部门与金融机构、金融机构与金融机构之间形成了越来越复杂的网络关系,具有与复杂网络系统相似的特征,比如节点的中心性、网络的连接密度等。理解这些特征对于分析地方公共债务风险的形成和传导具有重要作用。利用复杂网络相关理论提供的方法,研究地方公共债务风险的演变规律,有助于厘清不同经济主体在地方公共债务的风险网络中究竟发挥了什么作用,有效判别地方政府债务风险传染的路径和强度,对深化地方公共债务风险研究、提高地方公共债务风险管理水平具有重要意义。
本文的内容安排如下:首先,介绍财政金融风险的传统研究方法,并比较分析不同研究方法的局限性;其次,介绍复杂网络相关理论取得的若干较为成熟的研究成果(包括拓扑结构、生成模型以及网络类型等)在地方公共债务风险研究中的应用,并分析复杂网络与传统风险分析方法之间的关系;最后是总结和展望。
二、财政金融风险的传统研究方法
(一)金融风险的常见研究方法
1.在险价值法及其发展
在险价值法(Value at Risk,又称VaR模型)是投资组合理论的核心成果之一。VaR模型利用金融机构日度数据,通过方差分解、格兰杰因果检验以及脉冲响应分析等方法,评估资产、利率以及汇率等方面的金融风险。该方法能较好地解决内生变量和异方差问题,但也存在不足。例如,VaR模型对数据的正态分布假设往往与真实情况不符,无法体现分位点下方的左尾损失,不满足可加性要求,以及难以预测极端事件风险等。
针对以上缺陷,学者们提出了多种改进的VaR模型。Adrian和Brunnermeier(2016)构造了条件在险价值法(Conditional Value-at-Risk,CoVaR),通过计算某金融机构(或其他市场主体)在正常和陷入困境两种状态下的条件在险价值之差,反映该金融机构对系统性风险的贡献程度。Acharya等(2017)构造了边际期望损失(Marginal Expected Shortfall,MES),考察整个金融系统发生危机时,单个金融机构的风险贡献程度。Banulescu和Dumitrescu(2015)提出的成分期望损失法(CES)是在MES基础上将资产规模考虑在内,研究某金融机构对系统性风险的贡献程度。此外,Brownlees和Engle(2016)分析银行杠杆率对系统性风险的影响,采用衡量资本缺口的风险指数SRISK对MES进行了改进。
VaR及其拓展模型在计算金融机构对系统性风险的贡献程度不断精确,对描述系统性金融风险的传染效应具有重要价值。然而,不同的分析方法在衡量金融风险时具有特定的适用性和局限性。比如,CoVaR只考虑到机构与市场回报率的相关性,而没有考虑到其自身回报率的波动对系统性风险的影响(Acharya等,2017)。MES则忽略了银行规模及杠杆率对风险的影响(Banulescu和Dumitrescu,2015)。此外,SRISK方法将季频财报数据与日频收益率数据混合使用,其时效性与合理性也受到了一定质疑(Banulescu和Dumitrescu,2015)。
2.广义条件异方差模型
Bollerslev(1986)提出的广义条件异方差模型(GARCH),能够刻画金融市场间波动的动态相关及风险的传染效应。但由于该方法是基于模型残差的相关性,因此产生了诸多质疑,包括是否任何传染都能由共同冲击所引起,或是其他遗漏变量能否被模型捕捉等。近年来,不少学者利用GARCH模型的拓展模型如EGARCH、GJR-GARCH和DCC-GARCH等,研究金融风险传染效应(Nelson,1991;陈国进等,2021)。其中,EGARCH模型允许正负资产收益率对波动率有不对称的影响,克服了GARCH模型对系数必须非负的限制;GJR-GARCH是反映杠杆效应的波动率模型;DCC-GARCH模型允许变量之间相关性的动态变化,有利于把握不同风险间的动态相依性。
3.Copula函数
Copula函数用于刻画金融风险传染与金融市场结构之间的密切关系。与VaR模型或GARCH模型相比,Copula函数无须对收益率的运行规律作严格假设,能更好地捕捉金融市场的非线性相依与尾部相依行为,并且也可以描述金融市场的动态结构变化,进而分析金融风险传染机理。尽管Copula函数及其变种(时变Copula函数或变结构Copula函数)被频繁用来研究金融风险传染,这类方法在高维数据应用中面临难以控制计算复杂性等问题(Oh和Patton,2018)。
(二)地方公共债务风险的常见研究方法
现有文献对地方公共债务风险进行测算或评价,主要采用以下两种方法。
第一,风险指标法。通过构建能够反映地方公共债务风险程度的指标体系,对债务风险进行识别、排序、等级划分以及预警监测等。一类指标反映的是偿债压力、期限结构错配等即时风险,也可称为静态风险指标。例如,负债率和债务率是这方面常用的指标,衡量国民经济和财政收入对债务的即期承载能力(刁伟涛和傅巾益,2019)。部分文献基于税收收入(马海涛和吕强,2004)、土地出让收入(何杨和满燕云,2012)以及财政转移支付(郭玉清等,2015)等,构建税收偿债率、土地偿债率、转移支付依赖度等指标,多维检验地方公共债务的静态风险。另一类指标从债务增长对经济发展构成的影响、财政可持续性等角度评估风险的动态发展态势,多采用对比增速的方法进行衡量。例如,缪小林和伏润民(2012)采用经济债务弹性和居民收入债务弹性等指标,从动态角度衡量国民经济和居民收入的债务负担。
基于债务风险指标,已有研究积极利用多种其他方法深化地方公共债务风险的分析。例如,采用因子分析法检验地方公共债务风险的区域分布和变化特征(刁伟涛和傅巾益,2019);通过聚类分析法研究各类主体对地方公共债务的承担能力(李冠青,2018);基于层次分析法和熵值法构建地方公共债务风险预警体系(沈雨婷和金洪飞,2019)。部分文献还对具有非线性特征的复杂债务风险指标进行集成评价(刘骅和卢亚娟,2016)。然而,上述方法在具体应用中一定程度上依赖于研究者的一些主观判断。
第二,违约分析法。基于未定权益分析法的KMV模型,是目前常用于分析地方公共债务风险的一种方法。该方法通过相对债务规模与债务人的相对偿债能力,测算债务的违约距离和违约概率(苟文均等,2016)。后续研究不断改进KMV模型(韩立岩等,2003)。例如,洪源和胡争荣(2018)采用KMV修正模型,从流量和存量双重维度研究地方公共债务的违约风险。不少学者通过构建DSGE模型,从宏观角度探讨地方公共债务风险的传导机制以及量化债务违约风险(熊琛和金昊,2018;李力等,2020)。Logistic模型也是应用较为广泛的违约概率模型(曹勇等,2016)。例如,刁伟涛等(2019)基于内部评级法中违约概率、违约损失率和违约风险暴露等参数,构建Logistic违约概率模型,测算了中国地方政府一般债务和专项债务的风险情况。
此外,部分学者采用引力模型或空间杜宾模型(SDM)检验地方公共债务风险的空间外溢性(伏润民等,2017;沈丽等,2019)。
(三)财政金融风险传统研究方法的小结
总体来看,财政金融风险的传统研究方法各有侧重,互为补充。每种方法可以从某一层面或者某一维度对财政金融风险进行分析,但很难基于市场主体之间的关系揭示整体风险状况和风险传染过程。表1对财政金融风险的传统研究方法进行了归纳和比较。
表1 财政金融风险的传统研究方法比较
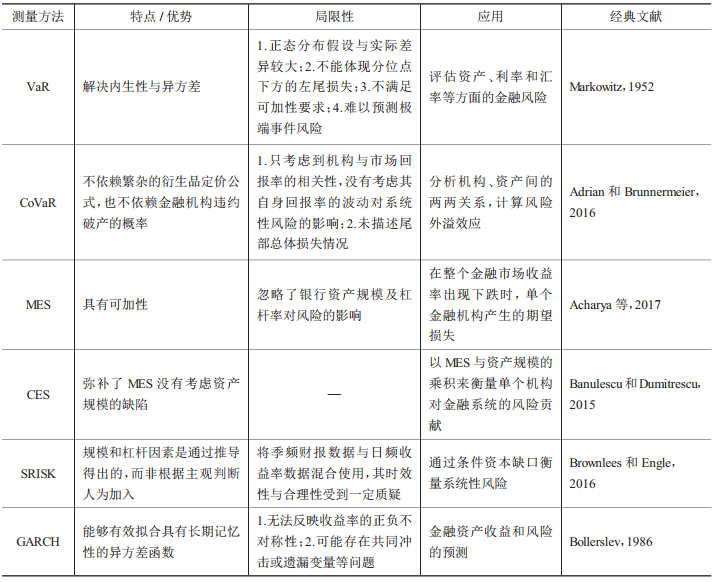
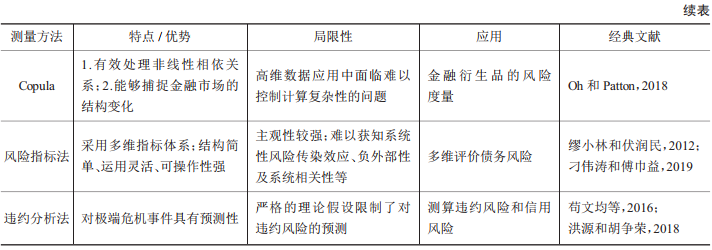
注:作者根据已有文献整理得到;表中部分方法在正文中做了阐述,另一些方法限于篇幅未展开分析。
三、复杂网络应用于地方公共债务风险研究的进展
正如前文所述,地方公共债务风险具有风险载体多元化、风险来源分散化等特点,可通过地方政府、商业银行、保险机构、证券市场等多个部门进行交互式传染,所以仅使用某一种传统研究方法进行风险分析往往是不科学、单一化和孤立式的。使用复杂网络分析地方公共债务风险的结构特征和传染路径,能克服传统研究方法存在的一些局限性。
(一)复杂网络概述
复杂网络是典型的跨学科分析方法,最早可追溯到18世纪数学家欧拉对“七桥问题”的研究。20世纪60年代,随机图理论的诞生意味着复杂网络理论进入了系统性研究的新阶段。20世纪末,Watts和Strogatz(1998)以及Barabási和Albert(1999)分别揭示了复杂网络具有“小世界”和“无标度”的特性。自此,复杂网络理论不再局限于数学的范畴,被广泛应用于物理学、工程技术以及经济管理等多个领域。
通俗地讲,复杂网络是将某个系统中的个体视为节点,个体之间的相关关系视为连边,进而研究网络系统的结构特征和动态变化规律。网络系统的复杂性主要体现在节点众多、连接结构复杂以及各种复杂性因素之间的相互影响。
(二)网络拓扑结构
复杂网络理论的研究者们借助数学里的拓扑知识,刻画复杂网络的若干核心特征,以便于将复杂网络应用于其他学科领域。这些特征包括:
1.节点的中心性
节点中心性是复杂网络分析中的重要内容,研究个体或者群体在网络结构中的重要性或者权重。在地方公共债务风险的网络研究中,节点中心性指标为判定个体(各类市场主体)的系统重要性提供了理论依据。典型的中心性分析指标包括度中心性(Degree Centrality)、介数中心性(Betweenness Centrality)和接近中心性(Closeness Centrality)。
(1)度中心性。度中心性分为绝对度中心性和相对度中心性。绝对度中心性方面,节点的绝对度值是指与该节点相连的边数的总和。在无向网络中,每条边的方向是相同的,而在有向网络中,节点的绝对度值是由入度(in-degree)和出度(out-degree)共同构成的,见式(1)。节点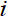 的入度(
的入度(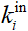 )是指网络中其他节点
)是指网络中其他节点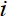 接入节点的边数和,节点
接入节点的边数和,节点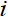 的出度(
的出度(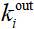 )是指由节点
)是指由节点 指向其他节点的边数和。
指向其他节点的边数和。
 (1)
(1)
基于入度和出度的概念,在地方公共债务风险网络中,不同个体的作用可分为以下三类:一是风险传播者,即个体的入度明显小于出度;二是风险接受者,即个体的入度明显大于出度;三是在网络中既是风险传播者也是风险接受者,即出度和入度的数值接近或相同。通过对风险网络中节点出入度的分析,有助于识别风险的溢出方向,进而准确分析风险传染的潜在路径(刘晓东和欧阳红兵,2019;陈梦根和赵雨涵,2019)。
相对度中心性(简称“度数”,采用DC表示)方面,考虑了网络规模的影响,对节点的绝对度值进行归一化处理,具体表示为节点的绝对度值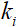 与网络中可能的最大度值之比,见式(2)。其中,N表示网络中节点的总数。
与网络中可能的最大度值之比,见式(2)。其中,N表示网络中节点的总数。
 (2)
(2)
(2)介数中心性。通过计算经过某个节点的最短路径的数量刻画该节点的重要性,简称介数(BC)。介数中心性反映了节点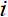 对于网络中各节点沿着最短路径传输风险的控制能力,其充当“桥梁”的次数越多,在风险网络中越重要。具体地,在一个包含N个节点的网络系统中,节点
对于网络中各节点沿着最短路径传输风险的控制能力,其充当“桥梁”的次数越多,在风险网络中越重要。具体地,在一个包含N个节点的网络系统中,节点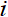 的介数中心性定义为:
的介数中心性定义为:
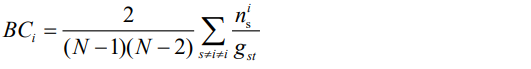 (3)
(3)
其中, 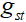 为从节点
为从节点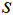 到节点
到节点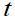 的最短路径的数目,
的最短路径的数目,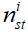 为从节点
为从节点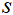 到节点
到节点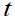 的
的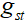 条最短路径中经过节点
条最短路径中经过节点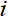 的最短路径的数目。
的最短路径的数目。
(3)接近中心性。接近中心性是通过计算任一节点到网络中所有其他节点距离平均值的倒数,衡量节点的重要性,简称接近数,用记号CCi来表示,见式(4)。其中,dij表示节点i到节点j的距离。一个具有高接近中心性的节点,说明其距离网络中的任意其他节点都较近,在空间上的体现是处于网络中心位置或附近。
 (4)
(4)
现有文献大多采用度中心性、介数中心性和接近中心性等指标识别金融机构或其他市场主体在风险网络中的系统重要性(欧阳红兵和刘晓东,2014)。一般而言,节点的度中心性越高,与其直接相连的节点数越多,通过该节点的最短路径也越多,该节点与其他节点之间的距离也越近,此时该节点的介数中心性和接近中心性也应越高。比如,沈丽和刘媛(2020)发现,在全球公共债务风险网络中,欧洲的多项中心性指标均相对较高,这意味着欧洲在公共债务风险的跨国传染网络中不仅与其直接相连的国家数较多,而且在该网络中发挥着“中心行动者”和“桥梁”的作用。
然而,采用不同的中心性指标对某一节点的系统重要性进行分析,得出的结果并不总是相同。以风筝型复杂网络为例(如图1所示),该网络中相对度中心性最高的是G点,即与其直接相连的节点数最多;介数中心性最高的是H点,其在网络中主要起到连接上下两部分的桥梁作用;接近中心性最高的是C点和E点,几何中心性的特征比较明显。

图1 风筝型复杂网络结构
注:作者参考汪小帆、李翔、陈关荣编著的《网络科学导论》(高等教育出版社2012年版,第161-162页)绘制。
财政金融风险的复杂网络分析结果进一步验证了上述规律。例如,何芳等(2020)通过构建地方政府债券网络,发现山东省的相对度中心性和接近中心性较高,而介数中心性偏低。这主要是因为山东省在全国地方政府债券网络中存在多条路径,使其与其他节点较为接近,同时与其相连的节点本身也属于高中心度的点,使得山东省的接近中心性较高,而由于山东省存在较多的冗余关联关系,导致其介数中心性偏低。李守伟和王虎(2021)也发现,在金融机构同业拆借网络中,节点的度值与债务排序并不总是一致的。表2分析了三项中心性指标反向变化时的具体含义。
表2 节点中心性指标的比较分析

注:作者根据相关资料整理得到。
2.其他特征
除了节点的中心性,网络密度、平均路径长度和聚类系数也是复杂网络的重要特征。限于篇幅,以下对上述特征进行简要说明,而着重阐述这些特征与节点的中心性结合起来在复杂网络分析中的应用情况。
网络密度是指网络中实际存在的边数M与最大可能的边数之比,用于刻画网络的稀疏性。在一个无向网络中,网络密度定义为:
 (5)
(5)
路径长度是指该路径中连边的数目,平均最短路径长度即任意两点间最少连边数的期望。在一个包含N个节点的复杂网络中,平均最短路径长度L定义为:
 (6)
(6)
聚类系数衡量邻节点之间联系的紧密程度,具体定义为实际邻节点之间的连边数与网络邻节点之间最大可能存在的连边数之比,如式(7)所示。
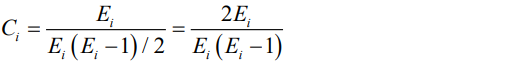 (7)
(7)
其中, Ei是节点 的ki个邻节点之间实际存在的边数。聚类系数的取值范围通常在[0,1]之间,越接近1,表明该节点与周围节点联系的紧密程度越高。
的ki个邻节点之间实际存在的边数。聚类系数的取值范围通常在[0,1]之间,越接近1,表明该节点与周围节点联系的紧密程度越高。
复杂网络中的节点度、平均最短路径、网络密度以及聚类系数等网络拓扑结构可以用来反映网络的连接结构(包括网络的稀疏程度等),而网络的连接结构与风险的形成、叠加和传染存在密切联系。相关文献主要可分为以下三类:其一,稀疏的网络结构更容易传染风险。Allen和Gale(2000)较早探索了风险传染与网络连接结构之间的关系,他们发现完全连接的金融网络最不容易出现传染性的违约风险。基本逻辑是网络节点之间丰富的连接能够保证有更多的交易对手分担违约损失,进而防止风险的进一步传染(Leitner,2005)。其二,紧密网络虽然能够降低单个市场主体的风险,但增加了市场主体之间的关联度,因此增加了风险传染的可能性。Degryse和Nguyen(2007)通过研究比利时银行系统传染风险的演变,发现从完整的网络连接结构(即所有银行都有对称联系)到“多货币中心”结构(货币中心与一些银行对称连接,而这些银行本身未连接在一起),降低了风险传染的可能性。Battiston等(2012)提出,随着信贷网络中交易对手数量的增加,网络中发生违约的概率也不断上升。这主要是由于个体金融脆弱度的反馈会放大最初冲击的影响,进而导致全面的系统性危机。鲍勤和孙艳霞(2014)也提出,中心—边缘的网络连接结构与完全连接的网络连接结构相比,会减小风险传染的范围,削弱风险传染程度。其三,网络连接结构与风险传染之间并非单调线性关系。Acemoglu等(2015)认为,当风险冲击小于阈值时,紧密网络对于抵御风险而言更加稳健;一旦风险冲击超过特定阈值,弱连接网络的脆弱性会大大降低。以银行系统为例,当出现大规模负面冲击时,银行系统的过剩流动性不足以吸收损失。在这种情况下,相对稀疏的网络结构能够保证损失由陷入困境的机构承担,从而保护系统的其他部分。
(三)复杂网络生成模型
为理解网络节点之间的联系以及网络行为的变化,需要对实际网络的结构特征进行深入分析,并在此基础上建立合理的网络模型,上述过程可称为复杂网络的生成模型。目前,复杂网络生成模型主要分为四类:规则网络、随机网络、小世界网络和无标度网络。常见的规则网络包括全局耦合网络、最近邻耦合网络和星形网络;ER随机图模型则是完全随机网络的典型代表。然而,大部分实际网络既不属于完全规则网络,也不属于完全随机网络,通常具有小世界和无标度特性。小世界网络具有较短的平均路径长度和较高的聚类系数。无标度网络的度分布服从幂律分布,具有两个重要特性:一是增长特性,即网络规模不断扩大;二是优先连接,即新的节点在加入网络时更倾向于与有更多连接的节点相连,例如,新论文通常倾向于引用权威文献。表3分析了以上几类网络生成模型的主要特征。
表3 四种网络模型基本特征的比较

注:作者根据相关资料整理得到。
关于风险网络的生成模型,一些文献是基于完全连接的网络结构假设条件(Upper和Worms,2004;李守伟等,2010)。然而,随着研究不断深入,发现财政金融风险网络的真实结构并非如此,完全连接的网络结构假设条件通常会严重高估风险传染的范围(Mistrulli,2011)。实际的风险网络通常是符合小世界和无标度特性的,比如,政府债务风险网络、全球股市收益率联动网络、信贷关系网络等(江若尘和陆煊,2014;李政等,2016)。无标度特性使得财政金融系统具有“稳健且脆弱”的倾向,即发生传染性违约的概率较低,但一旦发生特定风险事件,其危害是广泛且巨大的。具体地,由于无标度网络的大部分节点连通性较低,随机冲击导致发生传染性危机的可能性偏低,此时网络系统是稳健的;一旦高连通性的关键节点受到冲击,整个网络很可能迅速遭受严重破坏,此时网络系统是脆弱的。此外,也有文献发现,部分风险传染网络不具备无标度特性,这使得风险网络面对随机冲击时的脆弱性大大提高,极易发生大规模的传染性违约风险(韩瑜等,2020)。
(四)复杂网络的类型
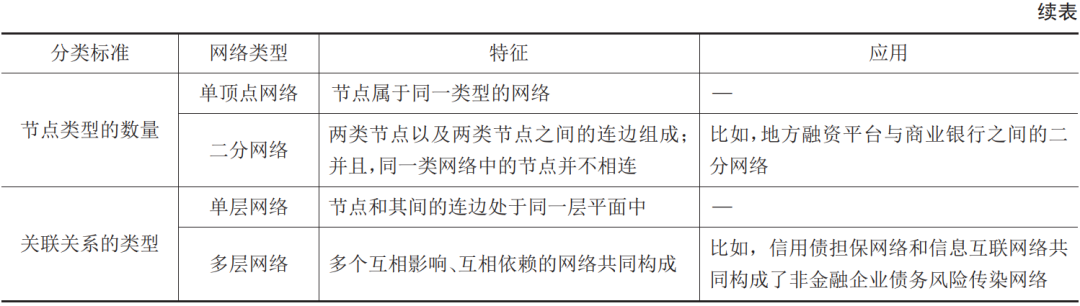
根据划分标准不同,复杂网络可分为多种类型。按照网络连边是否具有方向性,复杂网络可分为无向网络和有向网络。按照连边是否赋予权重,可分为无权网络和有权网络。无权网络重点描述节点之间是否存在相关关系,有权网络则具体量化相关关系的强度。按照节点类型的数量,复杂网络又可分为单顶点网络和二分网络等形式。其中,二分网络由两类节点以及两类节点之间的连边组成,并且同一类节点之间不相连。不少实际网络,比如地方政府与商业银行等金融机构之间的网络关系,呈现出明显的二分网络特征。何芳等(2020)构建以地方政府和银行为顶点的二分网络,研究地方政府债券网络的结构特征和系统性风险。He和Chen(2016)基于截面维度构建了地方融资平台和商业银行之间的二分网络,检验由土地财政风险引发的融资平台违约对银行体系的风险传染效应。此外,复杂网络还可分为单层网络和多层网络。单层网络是指节点和其连边处于同一层平面中;多层网络是由多个互相影响和共存的网络构成的。在地方公共债务风险网络系统中,市场主体之间往往表现出相互依赖、相互影响的多层网络特性。表4总结了不同类型复杂网络的特征及在地方公共债务风险网络研究中的应用。
表4 不同类型复杂网络的特征及应用

注:作者根据相关资料整理得到。
(五)复杂网络与传统风险研究方法的关系
复杂网络与传统风险分析方法并不是非此即彼、相互对立的,而是相辅相成、相互补充的关系。正如前文所述,任何一种风险分析方法都有其特定的适用场景和前提条件,复杂网络也不例外。传统风险分析方法能对复杂网络分析方法进行补充和完善,以更准确地测算和更深入地分析地方公共债务风险。一是网络分析方法依赖于节点之间的关联关系(即连边)。一旦关联关系不成立或无法识别,则不能称其为网络系统。实际中,在诸如金融网络等网络系统里,由于金融机构之间经济往来的数据往往难以获取,无法构建基于金融机构之间经济往来的关联关系,限制了对网络系统的深入分析。因此不少学者利用格兰杰因果检验法、向量自回归模型(VAR)、LASSO算法等传统风险分析方法,测算金融机构之间的经济往来情况,以构建金融机构之间的关联关系,并在此基础上形成风险网络,评估金融机构对系统性风险的贡献程度(刘晓东和欧阳红兵,2019;陈暮紫等,2020)。二是网络分析方法本身无法识别变量之间的因果效应。鉴于此,部分学者采用增量条件在险价值、边际期望损失等方法的测算结果作为系统性风险的代理变量,并以中心性指标等网络拓扑结构作为核心解释变量,通过计量分析方法检验网络结构与系统性风险之间的因果关系(宫晓莉等,2020)。
四、结语与展望
中国的地方公共债务风险包含财政风险与金融风险,容易形成不同风险的相互影响、不断叠加,从而导致系统性风险。通过对既有文献的梳理和研究,笔者发现,在财政金融风险的测度上,每一种传统的分析方法有其特定的前提条件和适用范围,很难准确反映财政系统与金融市场之间的风险传染路径以及风险的演变规律,更不可能只通过某一种风险分析方法完整地刻画财政金融风险交织传染的复杂性。此时,复杂网络作为一种新兴的风险分析方法,得到了越来越广泛的应用。通过对复杂网络拓扑结构、网络生成模型以及网络类型等方面的研究,可以有效识别地方公共债务风险传染路径和动态变化规律,能为防范化解地方公共债务风险提供新的经验证据。
正如前文所述,采用复杂网络研究财政金融风险已取得一些研究进展,而在专门的地方公共债务风险尤其是地方政府隐性债务风险领域,该方法的应用有待进一步深入。今后研究可在以下几个方面进行重点探索:第一,采用多项指标,综合衡量地方公共债务风险网络中的系统重要性个体,进而识别产生和传播风险的关键节点(可能是某家或某类金融机构、地方融资平台)。通过前文对网络中心性指标的分析,发现采用不同的中心性指标得出的系统重要性个体不尽相同,因此采用单一指标可能会产生片面化的分析结果。准确找到关键节点,并对其进行实时的风险监测与防控,能有效降低地方公共债务发生大范围风险传染的可能性。第二,深入分析地方公共债务风险网络的连接结构对风险传染的影响。根据前文分析可知,有关网络连接结构对风险传染影响的研究未达成一致结论。明确地方公共债务风险网络的连接结构对风险传染的具体影响,有助于监管部门制定更有针对性的法规和政策,强化或者分散相关市场主体之间的关联关系,提高风险网络面对随机冲击时的稳健性。第三,结合复杂网络和传统研究方法的各自优势,优化地方公共债务风险预警机制。在构建地方公共债务风险网络时,可结合传统研究方法,构建市场主体之间的关联关系,测度债务风险程度,有助于准确识别地方公共债务风险传染路径和演变过程,为实时监控和预防债务风险提供数据支持和理论依据。
文章来源:《财政科学》,2022年第6期。本文为原文节选。

