政策效应分析是经济学研究的重要领域之一。在定量评估某项政策所带来的经济效果或行为影响方面，国内外学者始终为内生性问题所困扰。为了检验因果关系，工具变量、匹配与加权估计等方法相继被开发并应用于实证研究。自20世纪80年代以来，双重差分法（difference-in-difference）开始在实证经济学领域兴起。双重差分法将制度与政策变化视为“外生冲击”，通过“准自然实验”的研究方法，构造处理组与对照组估计政策效应。由于其思路清晰、方法易用，逐渐被主流学界所接受并广泛应用于各研究领域。相比于普通多元线性回归，双重差分法不直接比较政策前后样本均值变化，而是从个体层面进行统计分析，既能控制样本间不可观测个体的异质性，又能控制不可观测因素的时间趋势，避免了解释变量的内生性问题，并得到无偏估计量（陈林和伍海军，2015）。然而，尽管从理论上分析双重差分法可以解决内生性问题，但是在实践中，政策的实施时间及对象往往是非随机的，内生分组问题将导致双重差分交互项估计量与被解释变量本身存在内生相关，那么双重差分的前提假设便不成立。此外，控制组被污染、样本异质性、自然实验与准实验概念界定不清等问题也对双重差分估计的准确性造成较大影响。此后，断点回归（regression discontinuity）开始被引入实证领域。由于在断点处被认为存在随机分组，一般将断点回归视为仅次于“自然实验”的一种内部有效性较强的准实验，也称之为“局部随机试验”（local randomized experiment）。断点回归可通过观测协变量在断点周围的分布以检验分组随机性，一定程度上解决了双重差分法分组内生性问题。但由于其因果推断仅存在于断点处，无法推广到全样本，因此外部有效性较弱。此外，断点回归依然受到样本不可观测异质性、带宽选择等因素的影响，并且需要满足一系列假设前提，适用范围有一定局限性。

另外，在政策制定过程中，诸多政策存在不连续性但并未构成准自然实验，由于不存在反事实组，基于外生冲击的双重差分法和断点回归法无法对政策进行分析检验。针对这一问题，聚束分析法（Bunching）应运而生。聚束分析法的核心优势在于无需自然实验构造反事实组，而是直接利用不受断点影响的样本分布模拟出断点周围样本分布的反事实曲线，进行结构参数估计，以评估政策对于行为反应的影响程度。并且，聚束分析法无需选取控制变量，可直接对目标变量通过统计分析模拟反事实曲线，避免了传统的回归分析中的遗漏变量问题。聚束分析法最初是为评估税收转移现象而开发（Saez，2010），随着各类数据的可得性提高，目前正逐步应用于税收以及其他学科领域中。

以往文献主要区分了两种不同概念的聚束：其一是由Saez（2010）和Chetty等（2011）提出的拐点（Kinks），该聚束类型的主要特征表现为预算集斜率的弯折；另一种则是由Kleven和Waseem（2013）开发的间断点（Notches），其特征表现为预算集斜率的弯折并同时伴随有预算线在弯曲处的跳跃。在税收领域问题的研究中，两者区别体现为在断点周围的平均税率是否存在显著跳跃。拐点在收入再分配政策中被广泛使用（例如超额累进税制、税收抵扣限额制度等），间断点则更多地应用于全额累进税制以及非税环境中。目前，随着理论与应用不断地完善和扩展，越来越多以聚束分析法为核心的研究成果发表在国际重要期刊上。在税收领域，聚束分析法被用于评估税收优惠政策（Saez，2010）、逃税（Kleven等，2011；Best等，2015）、税收对劳动供给影响（Chetty等，2011）、税收转移现象（LeMaire和Schjerning，2013）、应税收入弹性（Devereux等，2014；Bastani和Selin，2014；Kleven和Waseem，2013；Kleven和Schultz，2014）、财富税与财富积累（Jakobsen等，2020）、企业研发支出税收弹性（Chen等，2021）和房地产交易税（Kopczuk和Munroe，2015；Slemrod等，2017；Best和Kleven，2018）等。除税收制度外，聚束法的应用范围也被拓展到了各个领域的断点制度中，包括移民问题（Kleven等，2014）、养老金（Brown，2013；Manoli和Weber，2016）、医疗保险（Einava等，2015；Einava等，2017；Lu等，2019）、交通运输（Sallee和Slemord，2012；Traxler等，2018）、人口（Foremny等，2017）、住房抵押贷款（Anthony和DeFusco，2017）、企业正规化（Liu等，2019）和残障福利制度（Ruh和Staubli，2019）等领域中的断点制度问题均可使用聚束法进行评估分析。

在我国，类似的拐点和间断点同样出现于各领域中，但就当前而言，国内学者仅有张航和范子英（2019）对聚束分析法的基本原理进行介绍。在实证研究方面，樊勇等（2020）首次使用聚束分析法对中小企业所得税优惠政策进行了评估。王伟同等（2020）则以相同的政策分析了减税激励对于小微企业债务规模和融资成本的影响。但是，上述研究也存在着一定改进空间：（1）对聚束分析法的原理介绍不够清晰，对关键参数的推导与估计步骤不够全面细致；（2）估计方法与适用情形未进行区分，聚束区间存在大小之分，不同聚束区间长度下参数的估计式有显著差异；（3）未同时针对两类情形下的聚束现象开展分析评估，无法直观比较两类情形下聚束现象的异同。因此，本文旨在系统梳理聚束分析法的基本原理和估计方法，并以税收政策为例，针对我国政策断点问题进行分析评估，以期为聚束分析法在国内的应用提供经验指南。

后续部分的安排如下：第二部分介绍两类断点的基本原理；第三部分介绍聚束法的基本估计方法及模型改进；第四部分则立足于我国税收领域，对两类断点制度进行完整的聚束分析法检验；第五部分为结论及对聚束分析法的展望。

聚束分析法的核心在于通过高阶多项式回归，利用不受断点影响的样本分布模拟出断点周围样本分布的反事实曲线，通过实际分布曲线与反事实曲线的差异计算聚束值，进行政策效应评估，估计政策弹性，进一步计算社会福利变化。以聚束分析法的经典应用场景——累进所得税制为例，无论是超额累进所得税制，抑或是全额累进所得税制，当应纳税所得额超过临界点时，纳税人面临的边际税率会向上跳跃，边际税收负担的显著增长降低了劳动的边际收入。当越过累进所得税制临界点时，纳税人存在两种激励机制：（1）在替代作用的驱动下，降低劳动供给，减少税前收入至临界点附近；（2）瞒报应税收入，降低应税收入至临界点附近以减轻税收负担。无论是上述二者的何种情形，效应均表现为观测到的应税收入在临界点处集聚，最终呈现临界点周围的样本数目显著高于其余区间段的聚束型分布。累进所得税制下的断点类型可分拐点（Kinks）和间断点（Notches），分别对应超额累进制度和全额累进制度。超额累进税制下，由于边际税率的跳跃仅针对临界值以上的部分，平均税率并不会出现断层式上升，因此最终形成的聚束将以临界点为中心，两侧呈对称的“山峰型”分布。全额累进税制下，边际税率的跳跃将适用于全部应税收入，平均税率在临界点处会呈现断层式上升，导致部分临界点以上的样本严格转移到临界点以下，形成“断崖型”分布。本文以税收领域中的累进个人所得税制度为例，将聚束分析法在税收研究领域中应用的两类情形分别进行介绍。

在介绍聚束分析法的基本原理与估计方法后，下文将针对聚束现象中的拐点与间断点两种情形，以我国税收政策制定中出现的制度断点为例，结合理论分析对两类聚束情形进行实证检验，提供聚束分析法的实证案例，以期推动该方法在国内的普及。

(一)拐点情形下的聚束分析法运用——企业所得税业务招待费扣除限额政策效应估计

拐点情形下，聚束中的拐点在断点左右两侧斜率受制度影响会发生变化，表现为预算线的弯折。拐点多适用于税收领域中的超额累进税制和限额扣除等情形。以下部分以企业所得税中的业务招待费限额扣除政策为例，介绍由拐点产生的聚束现象。

1．政策背景和研究设计。

业务招待费是企业为业务经营的合理需要而支付的招待费用。2008年颁布的《企业所得税法实施条例》第四十三条规定：“企业发生的与生产经营活动有关的业务招待费支出，按照发生额的60%扣除，但最高不得超过当年销售（营业）收入的5‰。”此规定意味着当企业于年度内列支的业务招待费超过税法规定的税前扣除标准时，企业会在年度汇算清缴时发生纳税调增。业务招待费发生额的60%超过当年收入5‰的部分将无法按其实际发生额的60%进行扣除，这使得在以销售收入的“5‰”为分段点的两侧产生不同的税负差异。

设企业营业收入为TR，实际发生的业务招待费为EF，名义扣除额占收入比例为δ=60%·EF/TR，则不同业务招待费对应的业务区间扣除率如表1所示。

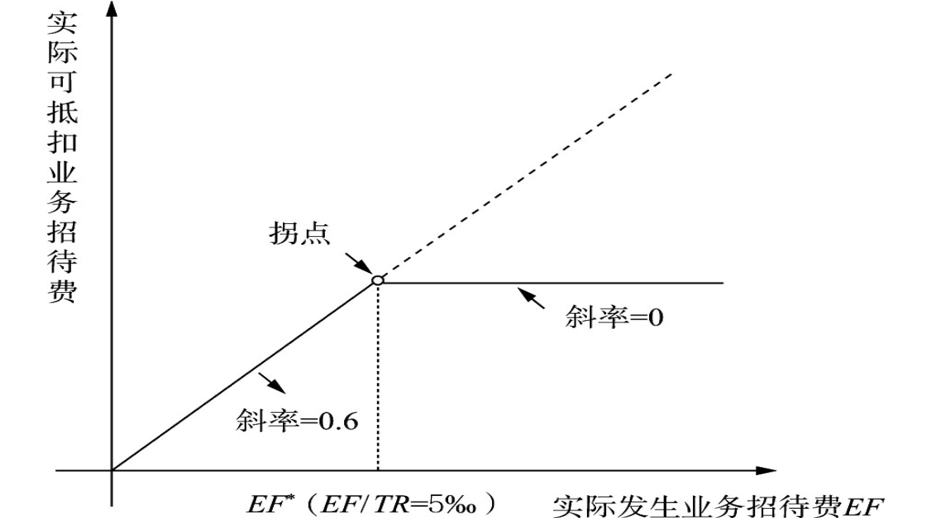
由表1和图3可知，处在δ∈[0，0.005]这一区间的企业，其业务招待费扣除额占实际发生业务招待费的比例为60%。处在δ∈(0.005，+∞)这一区间的企业，其业务招待费扣除以“5‰”为分段点：业务招待费未超过收入TR的5‰的部分按实际发生额EF的60%扣除；超过收入TR的5‰的对应部分其业务招待费不可扣除。基于上述分析，可以发现我国企业所得税中的业务招待费扣除限额政策与Saez（2010）分析的劳动所得税收抵免类似，属于典型的拐点：当δ≤0.005时企业发生的与生产经营活动有关的业务招待费支出，按照发生额的60%扣除；当δ＞0.005时，企业所享受的边际扣除率由60%降为0。

针对该扣除政策，在现实中企业有较强的激励调整业务招待费及营业收入，使得名义扣除额占收入的比例在5‰，实现最大化地享受扣除政策优惠，理论上在该点会产生显著的聚束现象。

为验证上述猜想，我们使用2011年至2014年全国税收调查数据进行实证分析。

2．业务招待费扣除限额5‰拐点附近的聚束现象。

图4是选取2011年至2014年各横截面全样本分析的图示结果。图中灰色线条为反事实估计曲线，黑色实线为观测到的实际分布曲线，竖直线为业务招待费扣除限额5‰的拐点位置。基准估计样本参数设定如下:组距为0.00001，分段点为0.005，样本拟合范围为［0.003，0.007］，聚束区域为［0.0049，0.0051］，重抽样的迭代次数设置为100次，高阶回归多项式次数为4。

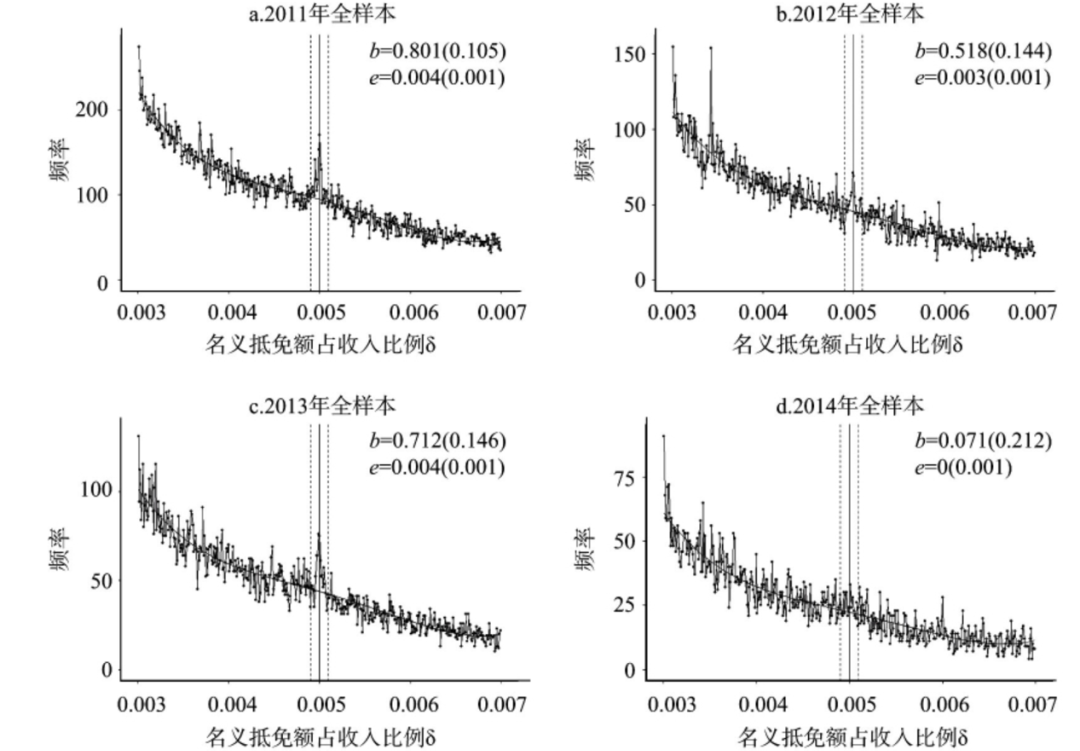
以图4a为例，该图描绘了在2011年全样本分布情况与反事实估计曲线。从图中可以看出，在扣除限额5‰处产生了明显的聚集式分布。相对聚束程度为0.801，应税收入弹性为0.004，估计结果均在1%的水平上显著，表明2011年处的临界点产生明显的聚束现象。超额水平估计值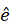=0.801意味着在指定的聚束区域内，观测值分布较下方的反事实分布值高出了80.1%。弹性估计值=0.004表明在集约边际下，由于临界点δ=0.005两侧的边际扣除率差异，计入业务招待费的边际扣除率每上升1%，企业向“5‰”调整δ的动机将上升0.004%。另外，2012—2014年的聚束图以及估计系数表明，除2014年外，其余年份中企业的“业务招待费/营业收入”这一指标在临界点“5‰”处均产生了明显的聚束。估计结果表明，有部分企业充分利用了税收优惠政策，通过调整业务招待费占收入的比例，最大化程度减少额外支出。

(二)间断点情形下的聚束分析法运用——小微企业所得税优惠政策效应估计

相较于拐点，间断点产生于选择集截距的离散变化，常见于全额累进税率的税制设计。以下部分以小微企业所得税税收优惠为例，介绍由间断点产生的聚束现象。

1．政策背景和研究设计。

虽然企业所得税并未像个人所得税一样采用累进税率，但是小微企业所得税优惠政策的存在却使得企业所得税在本质上类似于累进税率设计。在2019年之前，企业所得税本质上可以看作是全额累进税率。

具体而言，以2015年小微企业所得税优惠政策为例，认定条件见表3，按照2015年3月13日财政部和国家税务总局联合发布《关于小型微利企业所得税优惠政策的通知》（财税〔2015〕34号）的规定，认定条件分为三部分：从业人数、资产总额和应纳税所得额。只有三项条件均满足才能享受小微企业的税收优惠。其中，工业企业从业人数需要小于等于100人，其他企业小于等于80人；工业企业资产总额需要小于等于3000万，其他企业需要小于等于1000万。在满足以上两个条件的基础上，应纳税所得额小于等于20万时可以享受20%税率减半征收的优惠，即实际税率一般情况下为10%。应纳税所得额大于20万且小于等于30万时，则享受20%的优惠税率，应纳税所得额大于30万则不享受优惠，税率为25%。

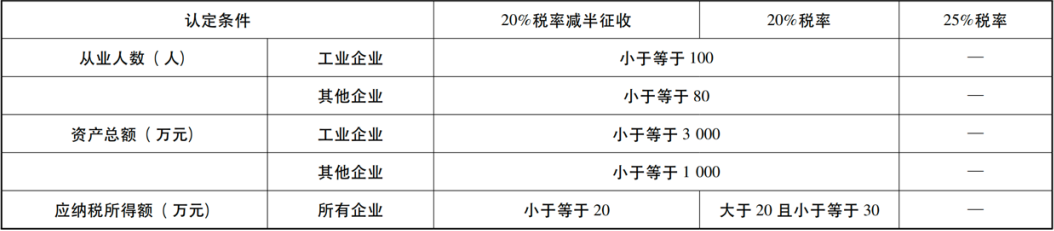
注：25%税率没有标识表示不满足上述三个条件中任意一个都适用25%的标准税率

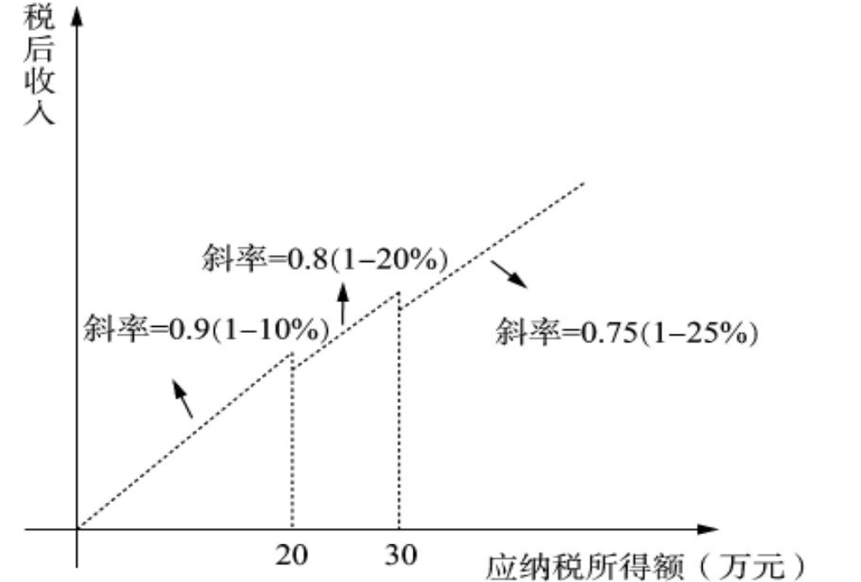
在这样的税率设计下，当企业满足从业人数和资产总额条件的情况下，企业所得税本质上是全额累进税率，其税率级次可以表示为图5。图中表示在满足其他条件的情况下，应纳税所得额的变动如何影响税后收入。在应纳税所得额20万处，税率由10%（20%减半征收）变为20%，斜率由0.9变为0.8，而在应纳税所得额30万处，税率由20%变为25%，斜率由0.8变为0.75。相较于拐点处两端相接的情况，在间断点处则存在向下的跳跃间断点。该部分展示的间断点处的聚束现象以20万处的间断点为例，在20万附近的企业，将应纳税所得额调整至20万以下可以额外享受10%的税收优惠，因此只要操作成本小于应纳税所得额的10%，企业就有动机调整自身的应纳税所得额。由于操作存在不确定性，一部分企业会调整成功，而一部分企业则会调整失败，仍然位于20万以上，从而形成在20万附近的聚束现象。

为了验证上述猜想，我们采用2015年全国税收调查数据，构建反事实分布，用以缓解相对聚束程度被高估的情况。

同时需要注意的是，由于在样本期间内，小微企业所得税税收优惠的落实程度有限，我们采用樊勇等（2020）类似的方式，仅将实际享受税收优惠的样本作为本文的样本。而没有享受税收优惠的企业由于没有调整的动机，不存在实质性的间断点，因此也就不存在间断点附近的聚束现象。

2.应纳税所得额20万间断点附近的聚束现象。

图6显示了应纳税所得额20万间断点附近的聚束现象及其估计结果，图中灰色线条为估计得到的反事实曲线，黑色实线为实际分布，竖直虚线为20万间断点的位置。样本拟合范围为12万到28万元，组距为1000元，聚束区域为19.7万到20.3万，高阶回归多项式次数为5次。图中右上角表示通过上文所述方法得到的相对聚束程度和应税收入弹性。

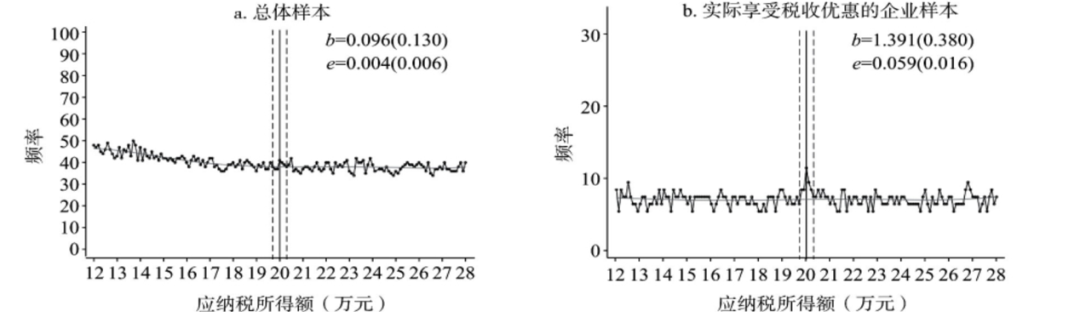
其中，左图是总体样本的聚束情况，并未发现显著的聚束现象，这是由于税收优惠政策的享受比例较低（樊勇等，2020），而右图是实际享受税收优惠的样本，从图中可以看到，在应纳税所得额20万元的间断点形成了明显的集聚现象，右上角的估计结果也表明聚束现象十分显著，相对聚束程度为1.391，应税收入弹性为0.059，均在1%的显著水平上显著。这表明有相当一部分企业通过调整应纳税所得额的方式获取额外的税收优惠，同时，也有相当一部分企业集聚在间断点右侧，表明也有很多企业调整失败，虽然有调整的动机，但没有达到预期目的，未享受到额外的税收优惠。

本文对聚束分析法从基本原理、估计方法及改进等方面进行了系统介绍，并以我国2008年企业所得税业务招待费抵扣限额政策和2015年小微企业所得税优惠政策为背景，结合大样本微观税收数据，分别讨论了拐点情形下和间断点情形下聚类分析法的实际运用情况，具体的结论与启示如下:

第一，聚束分析法是一种基于大样本微观数据下的实证研究方法，根据预算集在不连续点处的变化情况可分为拐点情形下的聚束现象（Kinks）和间断点（Notches）情形下的聚束现象。聚束分析法的具体应用是通过聚束值B以及相对聚束程度b的估计，计算对应政策点的政策弹性e，对政策效应进行定量评估。

第二，从方法论上看，目前的聚束分析法还是一个极简法（minimalist approach），该方法的估计有横截面数据即可，在数据利用率方面不如基于面板数据的双重差分法和断点回归法。另外，聚束往往只在局部出现，因此反事实分布拟合值外推也仅在小范围内进行。当数据量更丰富或局部估计情形不适用时，需要对模型进行改进，但目前相关的前沿研究仍然较少。Brown（2013）和Best等（2015a）提供了当聚束随时间改变时的弹性估计方法;Best等（2015b）则以房屋抵押贷款利率为研究对象，开发了一种新的面板数据聚束法。在将来，聚束分析法由于其数据的丰富性，面板数据下的聚束分析法应用范围将会愈加普及。

第三，本文结合相关税收数据将聚束分析法应用于我国的政策制度断点中，以企业所得税业务招待费扣除限额和小微企业所得税优惠政策为例，观测是否出现了显著聚束现象，在此基础上估计弹性e以及相对聚束程度b的具体数值，对其聚束现象的实际经济意义进行解释，并进行了相应的稳健性检验，以验证结果可靠性。

作为一类在国外学术界最近十年来兴起的实证研究方法，聚束分析法（Bunching）是近十年来国外学界兴起的微观经济实证研究方法。在大数据发展趋势下，聚束分析法具有其他方法所不具有的优势和应用前景，推动聚束分析法在国内应用，并不断改进，对我国经济学术研究和政策分析决策无疑具有重要的理论与现实意义。

文章来源：《中央财经大学学报》2021年第5期。本文为原文内容节选。